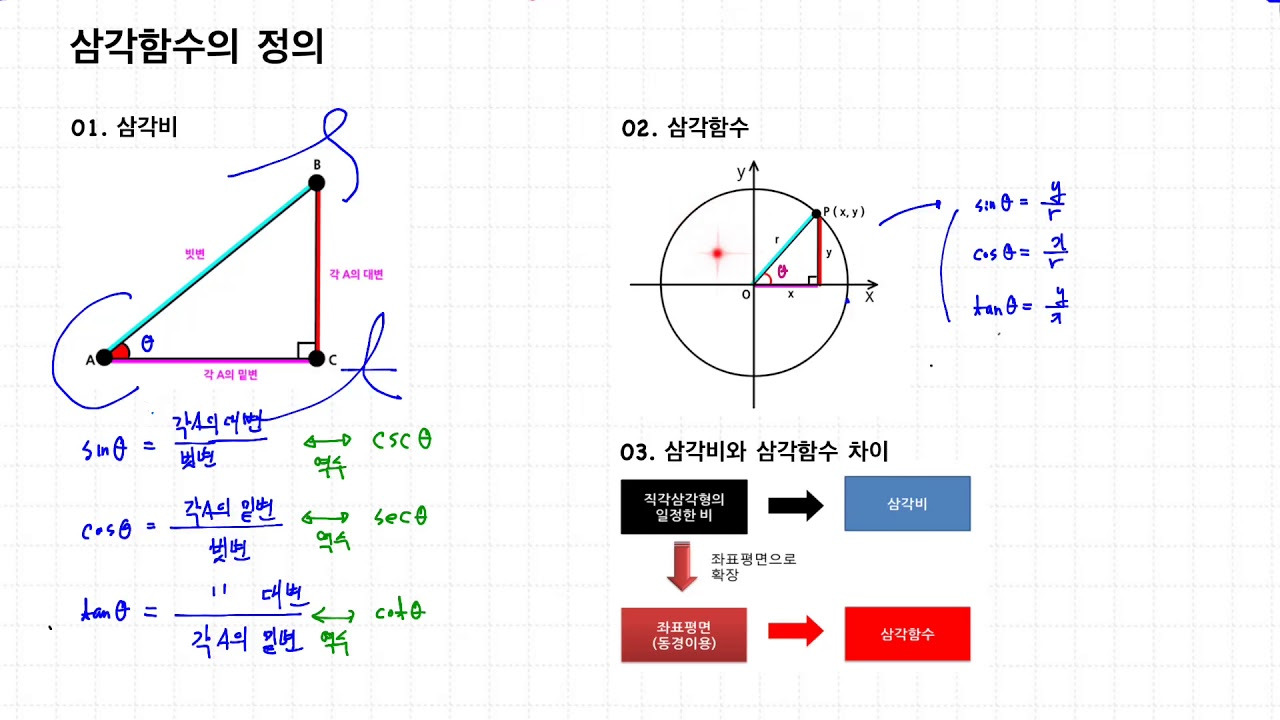
삼각함수 관련 질문각 자체의 값은 다르지만 사인값이나 코사인값 등이 같은 경우가 존재하나요? 존재한다면 그러한 경우와 원리를 설명해주시면 감사하겠습니다
삼각함수의 매력 중 하나는 특정 함수값이 다양한 각도에서 나타날 수 있다는 점입니다. 이는 주기성과 대칭성 덕분인데, 특히 사인(sin)과 코사인(cos) 함수에서는 두 가지 주요한 경우가 있습니다.
첫 번째로, 사인 함수는 주기적이며, 주기 2π2\pi를 가집니다. 즉, sin(x)=sin(x+2kπ)\sin(x) = \sin(x + 2k\pi) (여기서 kk는 정수)라는 성질이 있습니다. 이러한 성질 덕분에 동일한 사인 값을 가지는 서로 다른 각이 존재합니다. 예를 들어, sin(π6)=12\sin(\frac{\pi}{6}) = \frac{1}{2}인 경우, sin(5π6)=12\sin(\frac{5\pi}{6}) = \frac{1}{2}이므로 π6\frac{\pi}{6}와 5π6\frac{5\pi}{6}는 다른 각이지만 같은 사인 값을 가집니다.
두 번째로, 코사인 함수도 주기적이며, 이 역시 주기 2π2\pi를 가지고 있습니다. 하지만 코사인은 대칭성을 가지고 있어서 cos(x)=cos(−x)\cos(x) = \cos(-x)라는 성질이 있습니다. 이는 예를 들어, cos(0)=1\cos(0) = 1과 cos(2π)=1\cos(2\pi) = 1 또는 cos(π3)=12\cos(\frac{\pi}{3}) = \frac{1}{2}와 cos(−π3)=12\cos(-\frac{\pi}{3}) = \frac{1}{2} 같은 경우를 포함합니다.
이외에도 사인과 코사인 함수는 특정 각도에 대해 서로를 보완하는 관계에 있습니다. 즉, sin(x)=sin(π−x)\sin(x) = \sin(\pi - x)와 cos(x)=−cos(π−x)\cos(x) = -\cos(\pi - x)와 같은 관계가 성립합니다. 이로 인해 특정 값들이 다른 각도에서도 재현되는 것입니다.
따라서, 특정 사인 값이나 코사인 값을 가지는 여러 각들이 존재하는 이유는 삼각함수의 주기성과 대칭성 덕분입니다. 이러한 성질들은 삼각함수를 활용한 문제 해결 및 수학적 모델링에서 중요한 역할을 하며, 다양한 상황에서 유용하게 사용될 수 있습니다. 삼각함수의 특성을 잘 이해하면, 보다 깊이 있는 수학적 사고를 할 수 있는 기회가 될 것입니다.
티스토리 구독 해두시면 다양한 정보들을 무료로 구독해 보실 수 있어요.
